Two-stage CNN-based 3D Object Classification
In this post I’ll be discussing my final project for ECE 685: Deep Learning, a course I took at Duke University. For this project, Jiawei Chen and I proposed a two-stage algorithm to improve classification accuracy. You can find my Github repository for this blog here.
Convolutional Neural Networks (CNNs) have been used on 3D point clouds for object classification. However, due to the nature of the CNNs, classifiers, especially those CNN-based classifiers, are usually confused about objects that look alike. In this project, we propose a two-stage PointConv, a new method inspired by PointConv, which aims to improve the performance in the classes with a similar appearance. Experiments were carried out using ModelNet40 to train and test the system.
1. Project Goal
After reviewing a considerable amount of literature in 3D object classification, we noticed that among the state-of-the-art designs, CNN and its variants enjoyed great popularity among researchers due to its capability of capturing neighborhood relationships instead of focusing only on individual points in the clouds. However, it is also CNN's heavy reliance on detecting combinations of features that is responsible for models' confusion on classifying objects that look alike, such as recognize a table against a desk.

Thus, in this project, we propose an approach to specifically address the problem in which CNN-based deep learning geometric models get confused over similar-looking 3D objects, by employing a two-stage 3D object classifier. We combined the confusing categories into a new class. The first stage focusing on classifying the original unconfusing categories plus the newly formed one, and the second stage is specifically trained to classify those easily-confusing shapes. Then we aggregated the results from two classifiers based on the theory of conditional probability.
2. Two-stage algorithm
Rather than directly training a classifier to distinguish between all classes of objects, a two-stage classifier is proposed to improve prediction accuracy, especially for objects with a similar appearance.
Suppose there are \(K\) classes of objects in the dataset, namely \(C_1, \cdots, C_K\). Our aim is to build a classifier that can identify which class each object belongs to. We call \(\mathcal{C}\) a probabilistic classifier on \(\mathcal{X}\) if it provides an estimate for \(\mathbb{P}[x\in C_i\mid x\in \cup\mathcal{X}], C_i \in \mathcal{X}\) for each object \(x\), where \(\cup\mathcal{X} := \{\cup_{C\in \mathcal{X}} C\}\). For simplicity, we may denote this probability as \(\mathbb{P}_\mathcal{C}[x\in C_i]\) when \(\mathcal{X}\) is clear from context.
For any \(C \in \mathcal{F} \subset \mathcal{G}\), we have \(\mathbb{P}[x\in C\mid x\in \cup \mathcal{G}] = \mathbb{P}[x\in C\mid x\in\cup \mathcal{F}]\mathbb{P}[x\in \cup\mathcal{F}\mid x\in \cup\mathcal{G}].\)
This suggests that we can separate a classifier \(\mathcal{C}\) into two stages. Let \(\mathcal{F}_1,\cdots, \mathcal{F}_m\) be a partition on \(\mathcal{X} = \{C_1,\cdots, C_k\}\). By partition, we mean that \(\mathcal{F}_i\cap \mathcal{F}_j = \emptyset, i\neq j\), and \(\cup_{i=1}^m F_i = \mathcal{X}\). A classifier \(\mathcal{C}\) on \(\mathcal{X}\) is mathematically equivalent to a two-stage classifier, where the first stage is a classifier \(\mathcal{C}_1\) on \(\{\cup\mathcal{F}_1, \cdots, \cup\mathcal{F}_m\}\) and the second stage contains a classifier \(\mathcal{C}_{2i}\) for each \(\mathcal{F}_i\), defined on \(\{C_j: C_j\in \mathcal{F}_i\}\).
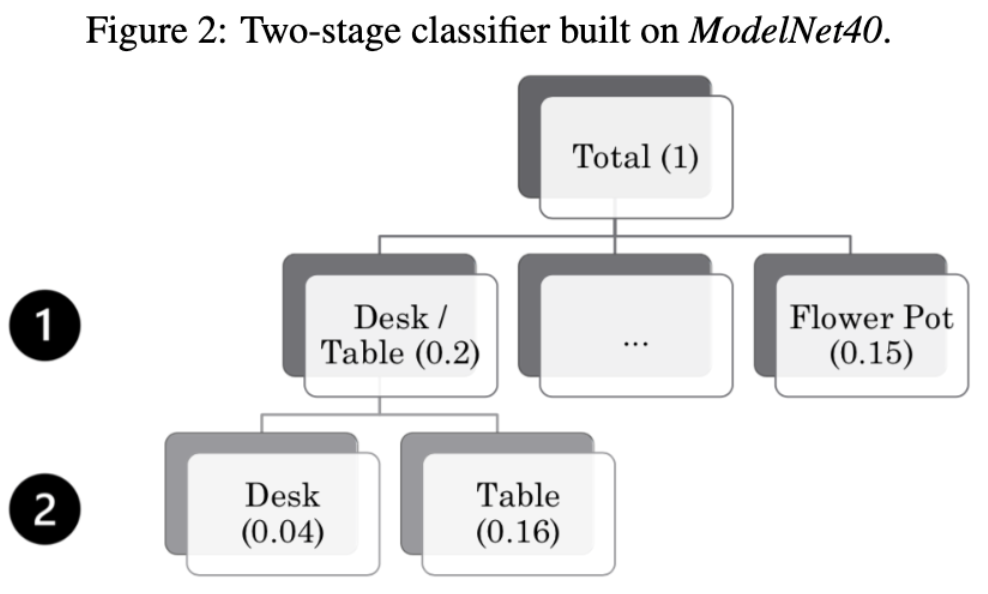
Although they are mathematically equivalent, breaking up a classifier into two stages may bring potential benefits practically as a classifier is more likely to achieve higher accuracy when the number of classes is reduced. One possible drawback of it, however, is that the increase in the number of classifiers may amplify the total error even though each single classifier achieves better accuracy. In lieu of this trade-off, we need to limit the number of classifiers, and maximize the potential boost in overall accuracy. Therefore, we only apply this two-stage classifier to classes which a one-stage classifier is likely to confuse. For example, the current classifier has a high error rate on table and desk, so we merge these two classes together in the first stage, and leave other classes as they are. In the second stage, we train a classifier that can distinguish table from desk. In this case, the two classifiers are trained independently.
Without loss of generality, we built a two-stage classifier (Figure 2) based on PointConv, which can better distinguish between tables and desks while still achieve comparable accuracy on the other classes of objects. Experiments were carried out using ModelNet40 to train and test the system.
3. Experimental Results
In order to evaluate the performance of our proposal in terms of accuracy, we conducted experiments on ModelNet40. We adjusted the implementation of PointConv with PyTorch using the SGD optimizer.
ModelNet40 contains 12,311 CAD models from the 40 categories. Unlike ModelNet10, the orientation of all the CAD models are not aligned. To alleviate this problem, Wenxuan Wu et al. proposed to predict the CAD model from three views. For each CAD model, three views were generated, and the final prediction is based on three predictions generated from the three views. We used the official split with 9,843 CAD models for training and 2,468 for testing.
For a fair comparison, we trained PointConv using SGD optimizer and evaluated its performance on the test set. Due to time constraints and limited computing resources, we trained both networks for 40 epochs. The test accuracy of the binary classifier (second-stage classifier) is 88% and the test accuracy of the first-stage classifier is 92.4%.

As a result of training our two-stage PointConv with a learning rate of 0.001 during 40 epochs using the ModelNet40 dataset, it obtained a success rate of 91.6%. With the same learning rate and the same number of iterations, PointConv achieved a success rate of 90.6%. As shown in Tabel 2, the accuracy in many classes has been improved.
However, while the accuracy in the class Desk has been improved by a bit, the accuracy in the class Table has not been improved. One possible reason is that the accuracy of the binary classifier is only 88%. Due to time constraints and limited computing resources, we might not select proper hyperparameters for the binary classifier. In addition, it might be helpful to train the two classifiers simultaneously. In this way, we believe the weight functions can be learned more effectively.
4. Discussion
In this project, we explored the applications of deep learning methods in 3D geometric data classification. We analyzed the recent breakthroughs to enable deep learning architectures to directly take point clouds as input and found the potential flaw of several state-of-the-art methods that are based on CNN. Then, based on the framework of PointConv network and the theory of conditional probability, we proposed a two-stage classifier to specifically address the problem in which CNN is unable to distinguish categories that look alike. By using our method, we have achieved a higher accuracy on the entire dataset.
In future work, we would like to find a proper optimizer so that we can minimize the loss with respect to the two classifiers simultaneously, and aggregate the two classifiers more effectively. In addition, we would like to try different binary classifiers and adopt a more efficient architecture on the second stage classifier to improve the model's performance.
Reference
[1] Belongie, S., Malik, J., & Puzicha, J. (2002). Shape matching and object recognition using shape contexts. IEEE transactions on pattern analysis and machine intelligence, 24(4), 509-522.
[2] Ben-Shabat, Y., Lindenbaum, M., & Fischer, A. (2017). 3d point cloud classification and segmentation using 3d modified fisher vector representation for convolutional neural networks. arXiv preprint arXiv:1711.08241.
[3] Garcia-Garcia, A., Gomez-Donoso, F., Garcia-Rodriguez, J., Orts-Escolano, S., Cazorla, M., & Azorin-Lopez, J. (2016, July). Pointnet: A 3d convolutional neural network for real-time object class recognition. In 2016 International Joint Conference on Neural Networks (IJCNN) (pp. 1578-1584). IEEE.
[4] Graham, B., & van der Maaten, L. (2017). Submanifold sparse convolutional networks. arXiv preprint arXiv:1706.01307.
[5] Johnson, A. E., & Hebert, M. (1999). Using spin images for efficient object recognition in cluttered 3D scenes. IEEE Transactions on pattern analysis and machine intelligence, 21(5), 433-449.
[6] Klokov, R., & Lempitsky, V. (2017). Escape from cells: Deep kd-networks for the recognition of 3d point cloud models. In Proceedings of the IEEE International Conference on Computer Vision (pp. 863-872).
[7] Maturana, D., & Scherer, S. (2015, September). Voxnet: A 3d convolutional neural network for real-time object recognition. In 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (pp. 922-928). IEEE.
[8] Qi, C. R., Su, H., Mo, K., & Guibas, L. J. (2017). Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 652-660).
[9] Qi, C. R., Yi, L., Su, H., & Guibas, L. J. (2017). Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Advances in neural information processing systems (pp. 5099-5108).
[10] Rusu, R. B., Blodow, N., & Beetz, M. (2009, May). Fast point feature histograms (FPFH) for 3D registration. In 2009 IEEE international conference on robotics and automation (pp. 3212-3217). IEEE.
[11] Tombari, F., Salti, S., & Di Stefano, L. (2011, September). A combined texture-shape descriptor for enhanced 3D feature matching. In 2011 18th IEEE international conference on image processing (pp. 809-812). IEEE.
[12] Wang, Y., Sun, Y., Liu, Z., Sarma, S. E., Bronstein, M. M., & Solomon, J. M. (2019). Dynamic graph cnn for learning on point clouds. Acm Transactions On Graphics (tog), 38(5), 1-12.
[13] Wang, Z., & Lu, F. (2019). VoxSegNet: Volumetric CNNs for semantic part segmentation of 3D shapes. IEEE transactions on visualization and computer graphics.
[14] Wei, L., Huang, Q., Ceylan, D., Vouga, E., & Li, H. (2016). Dense human body correspondences using convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 1544-1553).
[15] Wu, W., Qi, Z., & Fuxin, L. (2019). Pointconv: Deep convolutional networks on 3d point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 9621-9630).
[16] Wu, Z., Song, S., Khosla, A., Yu, F., Zhang, L., Tang, X., & Xiao, J. (2015). 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 1912-1920).
[17] Zhang, K., Hao, M., Wang, J., de Silva, C. W., & Fu, C. (2019). Linked dynamic graph CNN: Learning on point cloud via linking hierarchical features. arXiv preprint arXiv:1904.10014.